题目内容
【题目】已知函数y1=2kx+k与函数![]() ,定义新函数y=y2﹣y1
,定义新函数y=y2﹣y1
(1)若k=2,则新函数y= ;
(2)若新函数y的解析式为y=x2+bx﹣2,则k= ,b= ;
(3)设新函数y顶点为(m,n).
①当k为何值时,n有大值,并求出最大值;
②求n与m的函数解析式;
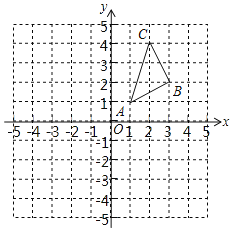
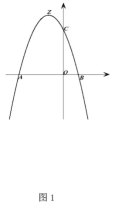
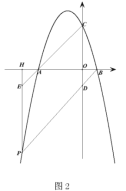
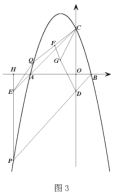
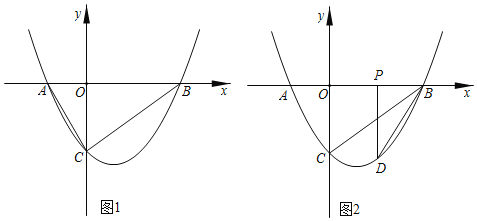
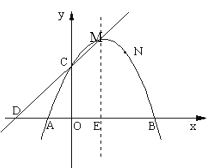
(4)请你探究:函数y1与新函数y分别经过定点B,A,函数![]() 的顶点为C,新函数y上存在一点D,使得以点A,B,C,D为顶点的四边形为平行四边形时,直接写出k的值.
的顶点为C,新函数y上存在一点D,使得以点A,B,C,D为顶点的四边形为平行四边形时,直接写出k的值.
【答案】(1)x2﹣6x+1;(2)5,﹣12;(3)①![]() ;② n=﹣m2﹣m+4;(4)
;② n=﹣m2﹣m+4;(4)![]() 或﹣
或﹣![]() 或﹣
或﹣![]() .
.
【解析】
(1)把![]() 代入
代入![]() 再把
再把![]() 代入新函数即可得到答案,
代入新函数即可得到答案,
(2)利用新函数的定义,结论关于![]() 的方程组即可得到答案,
的方程组即可得到答案,
(3)①利用新函数的定义,写出函数解析式,化为顶点式,利用二次函数的性质可得答案,②利用顶点坐标,消去
![]() 得到答案,
得到答案,
(4)先分别求解![]() 的坐标,设
的坐标,设![]() ,分三种情况讨论,利用平行四边形的对角线互相平分及中点坐标公式可得答案.
,分三种情况讨论,利用平行四边形的对角线互相平分及中点坐标公式可得答案.
解:(1)当k=2时,y1=2kx+k=4x+2,
∵函数![]() ,定义新函数y=y2﹣y1,
,定义新函数y=y2﹣y1,
∴y=x2﹣2x+3﹣4x﹣2=x2﹣6x+1,
故答案为:x2﹣6x+1;
(2)函数y1=2kx+k与函数![]() ,定义新函数y=y2﹣y1,
,定义新函数y=y2﹣y1,
∴新函数y的解析式为y=x2﹣2x+3﹣2kx﹣k=x2﹣2(k+1)x+3﹣k,
∵新函数y的解析式为y=x2+bx﹣2,
∴b=![]() ,3﹣k=﹣2,
,3﹣k=﹣2,
∴k=5,b=﹣12,
故答案为:5,﹣12;
(3)①由(2)知,新函数y=x2﹣2(k+1)x+3﹣k=(x﹣k﹣1)2﹣k2﹣3k+2,
∵新函数y顶点为(m,n),
∴![]()
∴![]() ,
,
当![]() 时,
时,![]() 的最大值
的最大值![]()
②由①知,![]()
将k=m﹣1代入n=﹣k2﹣3k+2得:
∴n=﹣m2﹣m+4;
(4)∵函数y1=2kx+k=k(2x+1),
当2x+1=0即x=![]() 时,y=0,
时,y=0,
∴A(![]() ,0),
,0),
∵新函数y=x2﹣2(k+1)x+3﹣k=x2﹣2(k+1)x﹣(k+1)+4=x2﹣(k+1)(2x+1)+4,
当2x+1=0,即x=![]() 时,y=
时,y=![]()
∴B![]() ,
,
∵函数![]()
∴C(1,2),
设D(c,d),
∵以点A,B,C,D为顶点的四边形为平行四边形,
∴①当BC与AD为对角线时,
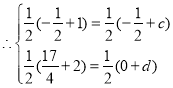
∴
∴D(1,![]() ),
),
将点D坐标代入新函数y=x2﹣2(k+1)x+3﹣k,
得,1﹣2(k+1)+3﹣k=![]() ,
,
∴![]()
②当AB与CD是对角线时,

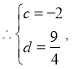
∴D(![]() ),
),
将点D坐标代入新函数y=x2﹣2(k+1)x+3﹣k
得,4+4(k+1)+3﹣k=![]() ,
,
∴k=![]() ,
,
③当AC与BD为对角线时,
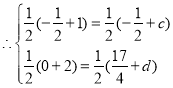
∴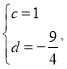
∴D(1,![]() ),
),
将点D坐标代入新函数y=x2﹣2(k+1)x+3﹣k
得,1﹣2(k+1)+3﹣k=![]() ,
,
∴k=![]() ,
,
即满足条件的k的值为![]() 或
或![]() 或
或![]() .
.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
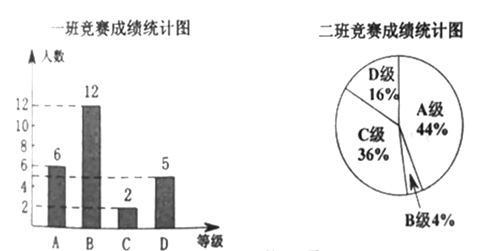
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.