题目内容
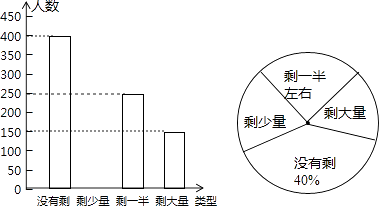
【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.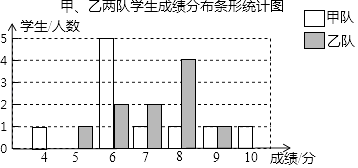
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .
【答案】
(1)6.8,7.5,6
(2)甲
(3)解:乙队的平均分高于甲队的平均分;
乙的方差小于甲队的方差,乙队的成绩比较稳定;
(4)![]()
【解析】解:(1)a= ![]() ×(4×1+6×5+7×1+8×1+9×1+10×1)=6.8,
×(4×1+6×5+7×1+8×1+9×1+10×1)=6.8,
b= ![]() =7.5,
=7.5,
c为6;
⑵因为甲的中位数为6,而乙的中位数为7,如果成绩属于中等偏上的位置,则应该为甲组;
⑷画树状图为:(甲队的优秀学生用A、A表示,乙队的优秀学生用B表示)
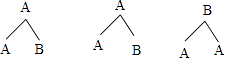
共有6种等可能的结果数,其中恰好同时选中的两人均为甲队学生的结果数为2,
所以恰好同时选中的两人均为甲队学生的概率= ![]() =
= ![]() .
.
所以答案是6.8,7,6;甲; ![]() .
.
【考点精析】通过灵活运用中位数、众数和概率公式,掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n即可以解答此题.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案【题目】(1)填写下表,观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0016 | 0.16 | 16 | 1600 |
|
(2)根据你发现的规律填空:
①已知:![]() =2.683 ,
=2.683 ,![]() 则
则![]() =_________,
=_________, ![]() =________
=________
②已知: ![]() =6.164,若
=6.164,若![]() =61.64, 则x=____________,
=61.64, 则x=____________,
(3)直接写出![]() 与a的大小.
与a的大小.