题目内容
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
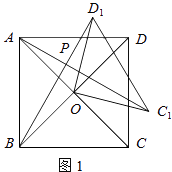
(1)如图1,若四边形ABCD是正方形.请直接写出AC1 与BD1的数量关系和位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,判断AC1与BD1的数量关系和位置关系,并给出证明;
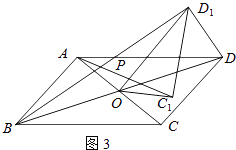
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1 , 设AC1=kBD1 , 请直接写出k的值和AC12+(kDD1)2的值.
【答案】
(1)解:AC1=BD1,AC1⊥BD1;
理由:如图1,
∵四边形ABCD是正方形,
∴OC=OA=OD=OB,AC⊥BD,
∴∠AOB=∠COD=90°,
∵△COD绕点O按逆时针方向旋转得到△C1OD1,
∴OC1=OC,OD1=OD,∠COC1=∠DOD1,
∴OC1=OD1,∠AOC1=∠BOD1=90°+∠AOD1,
在△AOC1和△BOD1中 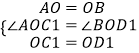 ,
,
∴△AOC1≌△BOD1(SAS);
∴AC1=BD1,
∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,
∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°,则AC1⊥BD1;
故AC1 与BD1的数量关系是:AC1=BD1;AC1 与BD1的位置关系是:AC1⊥BD1
(2)解:AC1= ![]() BD1,AC1⊥BD1.
BD1,AC1⊥BD1.
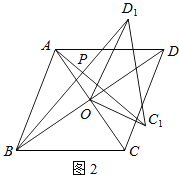
理由:∵四边形ABCD是菱形,
∴OC=OA= ![]() AC,OD=OB=
AC,OD=OB= ![]() BD,AC⊥BD.
BD,AC⊥BD.
∵△C1OD1由△COD绕点O旋转得到,
∴O C1=OC,O D1=OD,∠CO C1=∠DO D1.
∴O C1=OA,O D1=OB,∠AO C1=∠BO D1,
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
∴△AO C1∽△BOD1.
∴∠O AC1=∠OB D1.
又∵∠AOB=90°,
∴∠O AB+∠ABP+∠OB D1=90°.
∴∠O AB+∠ABP+∠O AC1=90°.
∴∠APB=90°.
∴AC1⊥BD1.
∵△AO C1∽△BOD1,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
即AC1= ![]() BD1,AC1⊥BD1
BD1,AC1⊥BD1
(3)解:如图3,与(2)一样可证明△AOC1∽△BOD1,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴k= ![]() ;
;
∵△COD绕点O按逆时针方向旋转得到△C1OD1,
∴OD1=OD,
而OD=OB,
∴OD1=OB=OD,
∴△BDD1为直角三角形,
在Rt△BDD1中,
BD12+DD12=BD2=144,
∴(2AC1)2+DD12=144,
∴AC12+(kDD1)2=36.
【解析】(1)由旋转的性质和正方形的性质得出对应边相等,各点旋转角相等可推出全等,再根据全等的性质可得出结论;(2)类比(1)的思路方法,可得相似,由对应边成比例,对应角相等可得结论;(3)类比(2),一样可证明△AOC1∽△BOD1,再由旋转的性质可推出△BDD1为直角三角形,再等量代换可得结论.
【考点精析】本题主要考查了相似三角形的判定与性质和旋转的性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.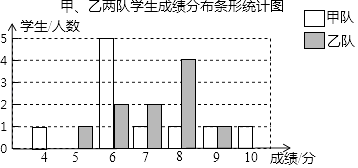
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .