��Ŀ����
��֪������x��һԪ���η���mx2����4m+1��x+3m+3="0" ��m��1����
��1����֤����������������ȵ�ʵ������
��2���跽�̵�����ʵ�����ֱ�Ϊx1��x2������x1��x2������y�ǹ���m�ĺ�������y=x1��3x2������������Ľ���ʽ��
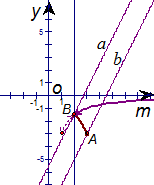
��3������2�������õĺ�����ͼ����ֱ��m=2����ಿ����ֱ��m=2���ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ������������µ�ͼ��ش𣺵�����m�ĺ���y=2m+b��ͼ�����ͼ��������������ʱ��b��ȡֵ��Χ��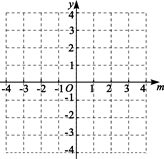
��1��֤������������2��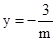 ����3��
����3��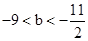 ��
��
���������������1�������ͻ�ƿ��������á�������ó�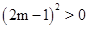 �ó�����0���Ӷ���������������ȵ�ʵ������
�ó�����0���Ӷ���������������ȵ�ʵ������
��2���������ʽ�ó�x�Ľ⣬��y=x1��3x2���������m�Ľ���ʽ��
��3����������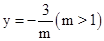 ��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ
��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ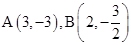 �����ֱ��
�����ֱ��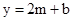 ����A��Bʱ��
����A��Bʱ��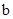 ��ֵ������֮�伴Ϊ����
��ֵ������֮�伴Ϊ����
��1��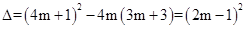 ��
��
��m��1��
��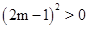
�������������ʵ����
��2��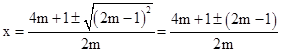
�������ֱ�Ϊ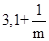 ��
��
��m��1��
��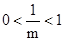 ����
����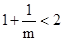 ��
��
��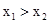 ��
��
��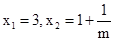 ��
��
��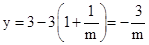 ��
��
��3����������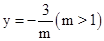 ��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ
��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ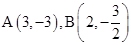 ��
��
��ֱ��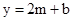 ����Aʱ��
����Aʱ��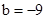 ��
��
��ֱ��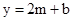 ����Bʱ��
����Bʱ��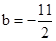 ��
��
��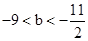 ��
��
���㣺1��һ�κ����ͷ����������ۺ��⣻2��һԪ���η��̸����б�ʽ��3����һԪ���η��̣�4�����۶ԳƵ����ʣ�

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�Ϊ����ѧ�������������εĸ߶ȶ��ǰ�һ���Ĺ�ϵ������Ƶģ��о���������������ĸ߶�Ϊ cm�����ӵĸ߶�Ϊ
cm�����ӵĸ߶�Ϊ cm����
cm���� Ӧ��
Ӧ�� ��һ�κ������±��г������������Ŀ����εĸ߶ȣ�
��һ�κ������±��г������������Ŀ����εĸ߶ȣ�
| | ��һ�� | �ڶ��� |
���Ӹ߶� ��cm�� ��cm�� | 40 | 37 |
�����߶� ��cm�� ��cm�� | 75 | 70 |
 ��
�� �ĺ�����ϵʽ��
�ĺ�����ϵʽ����2������һ�Ѹ�39 cm�����Ӻ�һ�Ÿ�78.2 cm�Ŀ����������Ƿ����ף�Ϊʲô��
 ��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��
��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��
 ��ͼ���ཻ�ڵ�A(2,5)�͵�B,��y���ཻ�ڵ�C(0��7).
��ͼ���ཻ�ڵ�A(2,5)�͵�B,��y���ཻ�ڵ�C(0��7). ��
�� .
.
 ��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����֪
��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����֪ ��
�� ����C��-2��m����ֱ��AB�ϣ�����������
����C��-2��m����ֱ��AB�ϣ����������� ��ͼ����C��
��ͼ����C�� ʱ������ʽ
ʱ������ʽ �Ľ⼯��
�Ľ⼯��
 ��x�ᡢy��ֱ���B�㡢A�㣬ֱ��
��x�ᡢy��ֱ���B�㡢A�㣬ֱ�� ��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C����SBCD�����Բֱ���ij��ȡ�
��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C����SBCD�����Բֱ���ij��ȡ�
 ,
, �ཻ�ڵ�
�ཻ�ڵ� ��
�� ��Ľ�������Ϊ
��Ľ�������Ϊ ��
�� ��Ľ�������Ϊ
��Ľ�������Ϊ �����ͼ�����������⣺��ÿС��4�֣���8�֣�
�����ͼ�����������⣺��ÿС��4�֣���8�֣� .
.
 ��0����BΪy���ϵ�һ�����㣬
��0����BΪy���ϵ�һ�����㣬 x+3�ϵ�һ�����㣬
x+3�ϵ�һ�����㣬
