题目内容
如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
(1)求这两个函数的解析式;
(2)当x取何值时, <
< .
.
(1)反比例函数的解析式为y= . 一次函数解析式为y=-x+7.
. 一次函数解析式为y=-x+7.
(2)当0<x<2或x>5时, <
< .
.
解析试题分析:(1)将点C、点A的坐标代入一次函数解析式可得k、b的值,将点A的坐标代入反比例函数解析式可得m的值,继而可得两函数解析式;(2)寻找满足使一次函数图象在反比例函数图象下面的x的取值范围.
试题解析:∵反比例函数y2= 的图象过点A(2,5)
的图象过点A(2,5)
∴5= ,m=10.即反比例函数的解析式为y=
,m=10.即反比例函数的解析式为y= .
.
∵一次函数y1=kx+b的图象过A(2,5)和C(0,7).
∴5=2k+7,k= -1 即一次函数解析式为y=-x+7.
解方程组 得
得 得
得
∴另一交点B的坐标为(5,2).
根据图象可知,当0<x<2或x>5时, <
< .
.
考点:反比例函数与一次函数的交点问题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,
①根据信息填表:
| | A地 | B地 | C地 | 合计 |
| 产品件数(件) | x | | 2x | 200 |
| 运费(元) | 30x | | | |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
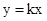 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
 (
( )与一次函数
)与一次函数 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2. 的值大于一次函数
的值大于一次函数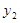 的值?
的值?

 (x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.