题目内容
如图，直线
,
相交于点
，与
轴的交点坐标为
，与
轴的交点坐标为
，结合图象解答下列问题：（每小题4分，共8分）
（1）求直线表示的一次函数的表达式；
（2）当为何值时，,表示的两个一次函数值都大于
.
（1）y=
x2；（2）x＞
.
解析试题分析：（1）因为直线l2过点A（2，3），且与y轴的交点坐标为（0，2），所以可用待定系数法求得函数的表达式．
（2）要求l1、l2表示的两个一次函数的函数值都大于0时x的取值范围，需求出两函数与x轴的交点，再结合图象，仔细观察，写出答案．
（1）设直线l2表示的一次函数表达式为y=kx+b．
∵x=0时，y=2；x=2时，y=3．
∴ 
∴ 
∴直线l2表示的一次函数表达式是y=x2.
（2）从图象可以知道，当x＞1时，直线l1表示的一次函数的函数值大于0．
当x2=0，得x=．
∴当x＞时，直线l2表示的一次函数的函数值大于0．
∴当x＞时，l1、l2表示的两个一次函数的函数值都大于0．
考点：两条直线相交或平行问题,一次函数的图象,待定系数法求一次函数解析式
夺冠金卷全能练考系列答案
的两根．
温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将n件产品运往A，B，C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示．设安排x件产品运往A地．
（1）当n=200时，
①根据信息填表：
| | A地 | B地 | C地 | 合计 |
| 产品件数（件） | x | | 2x | 200 |
| 运费（元） | 30x | | | |
②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？
（2）若总运费为5800元，求n的最小值．
许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋转位置从0度到90度（如图），燃气关闭时，燃气灶旋转的位置为0度，旋转角度越大，燃气流量越大，燃气开到最大时，旋转角度为90度．为测试燃气灶旋转在不同位置上的燃气用量，在相同条件下，选择燃气灶旋钮的5个不同位置上分别烧开一壶水（当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90），记录相关数据得到下表：
| 旋钮角度（度） | 20 | 50 | 70 | 80 | 90 |
| 所用燃气量（升） | 73 | 67 | 83 | 97 | 115 |
（1）请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律？说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
（2）当旋钮角度为多少时，烧开一壶水所用燃气量最少？最少是多少？
（3）某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气量．
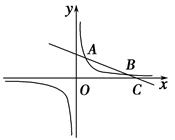
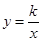的图象交于A（－2,6）和点B（4,n）