Question

【题目】如图1，矩形ABCD中，E是AD的中点，以点E直角顶点的直角三角形EFG的两边EF，EG分别过点B，C，∠F＝30°.

（1）求证：BE＝CE

（2）将△EFG绕点E按顺时针方向旋转，当旋转到EF与AD重合时停止转动.若EF，EG分别与AB，BC相交于点M，N.（如图2）

①求证：△BEM≌△CEN；

②若AB＝2，求△BMN面积的最大值；

③当旋转停止时，点B恰好在FG上（如图3），求sin∠EBG的值.

Answer 1

【答案】（1）详见解析；（2）①详见解析；②2；③.

【解析】

（1）只要证明△BAE≌△CDE即可；

（2）①利用（1）可知△EBC是等腰直角三角形，根据ASA即可证明；

②构建二次函数，利用二次函数的性质即可解决问题；

③如图3中，作EH⊥BG于H．设NG=m，则BG=2m，BN=EN=m，EB=m．利用面积法求出EH，根据三角函数的定义即可解决问题.

（1）证明：如图1中，

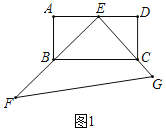
∵四边形ABCD是矩形，

∴AB=DC，∠A=∠D=90°，

∵E是AD中点，

∴AE=DE，

∴△BAE≌△CDE，

∴BE=CE．

（2）①解：如图2中，

由（1）可知，△EBC是等腰直角三角形，

∴∠EBC=∠ECB=45°，

∵∠ABC=∠BCD=90°，

∴∠EBM=∠ECN=45°，

∵∠MEN=∠BEC=90°，

∴∠BEM=∠CEN，

∵EB=EC，

∴△BEM≌△CEN；

②∵△BEM≌△CEN，

∴BM=CN，设BM=CN=x，则BN=4-x，

∴S△BMN=x（4-x）=-（x-2）2+2，

∵-＜0，

∴x=2时，△BMN的面积最大，最大值为2．

③解：如图3中，作EH⊥BG于H．设NG=m，则BG=2m，BN=EN=m，EB=m．

∴EG=m+m=（1+）m，

∵S△BEG=EGBN=BGEH，

∴EH==m，

在Rt△EBH中，sin∠EBH=．