题目内容
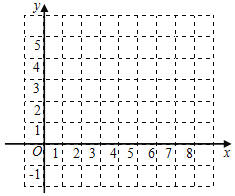
【题目】定义：在平面直角坐标系中，我们将横、纵坐标都是整数的点称为“整点”．若抛物线y＝ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”，则a的取值范围是_____．
【答案】
【解析】
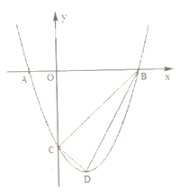
如图所示，
，图象实心点为8个“整点”，则符合条件的抛物线过点A、B之间
不含点
，即可求解．
解：
，
故抛物线的顶点为：
；
抛物线y＝ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”，
∴，如图所示，图象实心点为8个“整点”，
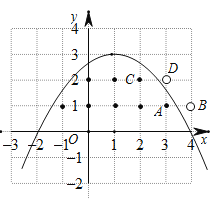
则符合条件的抛物线过点
和点
上方，并经过点
和点
下方，
当抛物线过点上方时，
，解得： 
；
当抛物线过点上方时，
，解得： 
；
当抛物线过点下方时，
，解得： 
；
当抛物线过点
下方时，
，解得： 
；
∵四个条件同时成立，∴
故答案为：．
练习册系列答案
相关题目
【题目】已知y＝|y1|+y2﹣1，其中y1＝x﹣3，y2与x成反比例关系，且当x＝2时，y2＝3．
（1）根据给定的条件写出y与x的函数表达式及自变量x的取值范围： ．
（2）当x＞0时，根据y与x的函数表达式，选取适当的自变量x的值，完成下表，并根据表中数据，在平面直角坐标系xOy中描点，画出该函数x＞0时的图象．
x | …… | …… | |||||||
y | …… | …… |
（3）当x＞0时，结合函数图象，解决相关问题：估计y＝﹣
x+5时，x的值约为 ．（保留一位小数）
