题目内容
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
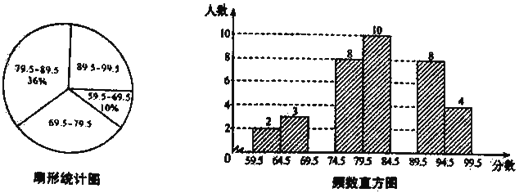
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
【答案】(1)50,30%;(2)不能,理由见解析;(3)P=![]()
【解析】(1)由直方图可知59.5~69.5分数段有5人,由扇形统计图可知这一分数段人占10%,据此可得选手总数,然后求出89.5~99.5这一分数段所占的百分比,用1减去其他分数段的百分比即可得到分数段69.5~79.5所占的百分比;
(2)观察可知79.5~99.5这一分数段的人数占了60%,据此即可判断出该选手是否获奖;
(3)画树状图得到所有可能的情况,再找出符合条件的情况后,用概率公式进行求解即可.
(1)本次比赛选手共有(2+3)÷10%=50(人),
“89.5~99.5”这一组人数占百分比为:(8+4)÷50×100%=24%,
所以“69.5~79.5”这一组人数占总人数的百分比为:1-10%-24%-36%=30%,
故答案为:50,30%;
(2)不能;由统计图知,79.5~89.5和89.5~99.5两组占参赛选手60%,而78<79.5,所以他不能获奖;
(3)由题意得树状图如下
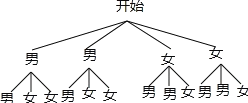
由树状图知,共有12种等可能结果,其中恰好选中1男1女的共有8种结果,故P=![]() =
=![]() .
.

【题目】秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分 数 段 | 频数 | 频率 |
60≤x<70 | 9 | a |
70≤x<80 | 36 | 0.4 |
80≤x<90 | 27 | b |
90≤x≤100 | c | 0.2 |
请根据上述统计图表,解答下列问题:
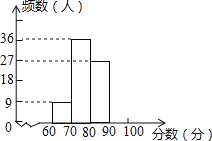
(1)在表中,a= ,b= ,c= ;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?