Question

【题目】如图，已知△ABC中，AB＝AC，把△ABC绕A点顺时针方向旋转得到△ADE，连接BD，CE交于点F．

（1）求证：△AEC≌△ADB；

（2）若AB＝，∠BAC＝45°，当四边形ADFC是菱形时，求BF的长．

Answer 1

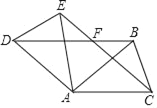
【答案】（1）证明见解析（2）2-

【解析】

（1）由把△ABC绕A点顺时针方向旋转得到△ADE，可得AD＝AE＝AB＝AC，∠DAE＝∠BAC，则∠DAB＝∠EAC，可证△AEC≌△ADB；

（2）由AC∥DB，可得∠ABD＝∠BAC＝45°可得△ADB为等腰直角三角形，可求DB的长度，且DF＝AC＝AB＝，所以BF的长可求．

（1）∵把△ABC绕A点顺时针方向旋转得到△ADE，

∴AD＝AE＝AB＝AC，∠DAE＝∠BAC，

∴∠DAB＝∠EAC，且AD＝AB，AE＝AC，

∴△AEC≌△ADB；

（2）∵ADFC是菱形，

∴AD＝AC＝CF＝DF＝AB＝，AD∥CF，DF∥AC，

∴∠DBA＝∠BAC＝45°，

∵AD＝AB，

∴∠DBA＝∠BDA＝45°，

∴∠DAB＝90°，

∴BD2＝AD2+AB2，

∴BD＝2，

∴BF＝2﹣.