��Ŀ����
����Ŀ����ͼ����֪��ABC�У�AB��AC��5��BC��6����O�DZ�BC�ϵĶ��㣬�Ե�OΪԲ�ģ�OBΪ�뾶��ԲO����AB���ڵ�D������D����ODP����B������AC�ڵ�P����ԲO���E����OB��x��
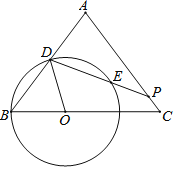
��1������P���C�غ�ʱ����PD�ij���
��2����AP��EP��y����y����x�Ľ���ʽ��������
��3������OP����OP��ODʱ�����ж��Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ��
���𰸡���1��5����2��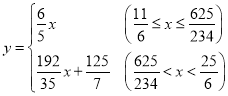 ����3���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ
����3���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ
��������
��1������OB=OD��AB=AC�Լ���ADO=��B+��BOD=��ODP+��ADP�����Ŀ������ODP=��B���������
��2���ֵ�P��C�غϣ�P��E�غϣ�D��A�غ�����������ۣ������Ӧ��xֵ���ٷ���������ֱ������Ӧ�Ľ���ʽ
��3������OP�������Բ�İ뾶��Բ�ľ༴���ж���Բ��λ�ù�ϵ
��1����ͼ1�У���AH��BC��H��CG��AB��G��
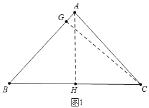
��AB��AC��5��AH��BC��
��BH��CH��3��AH��4��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ͼ2�У�����P��C�غ�ʱ��
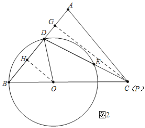
��OB��OD��
���B����ODB����ACB��
�ߡ�ADO����B+��BOD����CDO+��ADP����ODP����B��
���ADP����BOD����BAC��
��PA��PD��5��
���ⷨ����֪��A��180�㩁2��B��ֻҪ֤����ADP��180�㩁2��B���ɽ�����⣩
��2����ͼ2�У���CG��AB��G��OH��BD��H��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ͼ3�У���P��E�غ�ʱ����EG��AD��G��
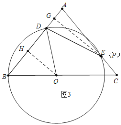
���ݶԳ��Կ�֪��B��E����ֱ��OD�Գƣ�
��![]() ��
��
��![]() ��
��
��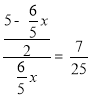 ��
��
���![]() ��
��
����D��A�غ�ʱ![]() ��
��
��![]() ��
��
��![]() ʱ����ͼ4�У�
ʱ����ͼ4�У�
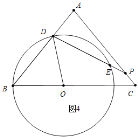
��![]() ��
��
��![]() ��
��
��![]() ʱ����ͼ5�У���PG��AB��G��
ʱ����ͼ5�У���PG��AB��G��
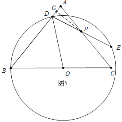
��![]() ��
��
��![]() ��
��
��![]() ��
��
����������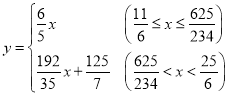 ��
��
��3����ͼ6�У�����OP��
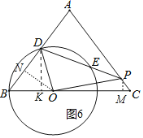
����OP����DK��OB��ON��BD��PM��BC��M����ON��4k������֪OB��DO��5k��BN��DN��3k��
![]() ��
��
�ɡ�DOK�ס�OPM�ɵ�![]() ���ɵ�
���ɵ�![]() ��
��
��![]() k��
k��
���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ��

����Ŀ��ijУѡ������˶�Ա�μӱ������ס�����������ͬ��������������и�![]() �Σ����еĻ�������Ϊ������10���������������
�Σ����еĻ�������Ϊ������10���������������
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�� |
|
|
|
|
|
|
|
|
|
|
�� |
|
|
|
|
|
|
|
|
|
|
��1����![]() Ϊ��ֵʱ��ѡ����ȥ�μӱ��������ʣ���˵�����ɣ�
Ϊ��ֵʱ��ѡ����ȥ�μӱ��������ʣ���˵�����ɣ�
��2���������������о�����![]() ������ѡ��˭ȥ�μӱ��������ʣ���˵�����ɣ�
������ѡ��˭ȥ�μӱ��������ʣ���˵�����ɣ�