题目内容
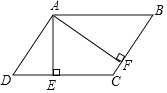
【题目】如图，在平行四边形ABCD中，AE⊥CD，垂足为E，AF⊥BC，垂足为F，AD＝4，BF＝3，∠EAF＝60°，设
，如果向量
，那么k的值是_____．
【答案】
【解析】
本题考查的是平行四边形的性质、解直角三角形与平面向量，根据平行四边形的性质求出∠B=∠D=60°，再利用正余弦定理，解出DE、AB的值，再利用平面向量平行向量两个方向相反的非零向量的知识解答即可
∵AE⊥CD、AF⊥BC，
∴∠AEC＝∠AFC＝90°，
∵∠EAF＝60°，
∴∠C＝360°﹣∠AEC﹣∠AFC＝120°，
∵四边形ABCD是平行四边形，
∴∠B＝∠D＝60°，
∴
，
，
则CE＝CD﹣DE＝AB﹣DE＝6﹣2＝4，
∵AB∥CD，且AB＝CD，
∴
，
故答案为： ．
练习册系列答案
阅读快车系列答案
相关题目
