题目内容
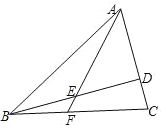
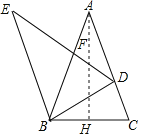
【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知![]() ,AC=5,那么△DBF的面积等于_____.
,AC=5,那么△DBF的面积等于_____.

【答案】![]() .
.
【解析】
根据相似三角形的性质得到![]() ,∠CBD=∠A,得到CD=2,AD=3,根据旋转的性质得到∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,得到∠EBF=∠A,根据平行线的判定和性质得到∠ADF=∠E,等量代换得到∠E=∠EBF=∠A=∠ADF,根据等腰三角形的判定得到EF=BF,AF=DF,得到AB=DE=AC=5,根据相似三角形的性质得到
,∠CBD=∠A,得到CD=2,AD=3,根据旋转的性质得到∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,得到∠EBF=∠A,根据平行线的判定和性质得到∠ADF=∠E,等量代换得到∠E=∠EBF=∠A=∠ADF,根据等腰三角形的判定得到EF=BF,AF=DF,得到AB=DE=AC=5,根据相似三角形的性质得到![]() ,过A 作AH⊥BC于H,于是得到结论.
,过A 作AH⊥BC于H,于是得到结论.
∵△BDC∽△ABC,
∴![]() ,∠CBD=∠A,
,∠CBD=∠A,
∴![]() ,
,
∵![]() ,AC=5,
,AC=5,
∴CD=2,
∴AD=3,
∵将△ABC绕点B按逆时针方向旋转得到△EBD,
∴∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,
∴∠EBF=∠CBD,
∴∠EBF=∠A,
∴BE∥AC,
∴∠ADF=∠E,
∴∠E=∠EBF=∠A=∠ADF,
∴EF=BF,AF=DF,
∴AF+BF=EF+DF,
即AB=DE=AC=5,
∵AD∥BE,
∴△ADF∽△BEF,
∴![]() ,
,
∴![]() ,
,
过A 作AH⊥BC于H,
∴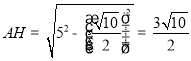 ,
,
∵![]() ,
,
∴△DBF的面积=![]() .
.
故答案为:![]() .
.

【题目】为了庆祝“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
| 30 | 0.15 |
|
| 0.45 |
| 60 |
|
| 20 | 0.1 |
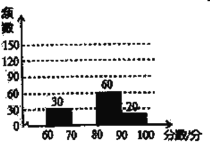
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽査了_______名学生;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角的度数是________;
所对应扇形的圆心角的度数是________;
(4)全校共有600名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?