题目内容
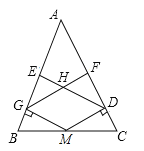
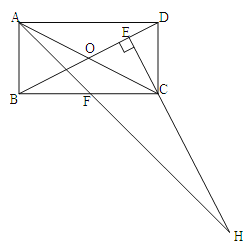
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
【答案】C
【解析】
试题根据矩形的性质可得OA=OB=OC=OD,由AD=![]() ,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
根据已知条件不能推出AF=FH,故①错误;
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=![]() ,AB=1,
,AB=1,
∴tan∠ADB=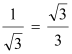 ,
,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,故②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,故③正确;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=![]() DO=
DO=![]() BD,
BD,
∴BE=3ED,故④正确;
∴正确的有3个,
故选C.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案