题目内容
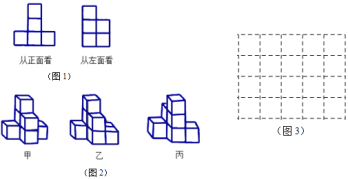
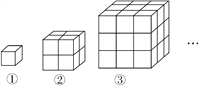
【题目】如图，观察由棱长为1的小立方体摆成的图形，寻找规律：如图①中共有1个小立方体，其中1个看得见，0个看不见；如图②中共有8个小立方体，其中7个看得见，1个看不见；如图③中共有27个小立方体，其中19个看得见，8个看不见，…
(1)第6个图形中，看得见的小立方体有___个；
(2)猜想并写出第n个图形中看不见的小立方体的个数.
【答案】（1）91；（2）(n－1)3个．
【解析】由题意可知，共有小立方体个数为序号数×序号数×序号数，看不见的小正方体的个数=（序号数-1）×（序号数-1）×（序号数-1），看得见的小立方体的个数为共有小立方体个数减去看不见的小正方体的个数．
(1)当n＝1时，看不见的小立方体的个数为(1－1)3＝0(个)；
当n＝2时，看不见的小立方体的个数为(2－1)3＝1(个)；
当n＝3时，看不见的小立方体的个数为(3－1)3＝8(个)；
…
当n＝6时，看不见的小立方体的个数为(6－1)3＝125(个)，
∴看得见的小立方体有63－125＝216－125＝91(个)；
(2)第n个图形中看不见的小立方体的个数为(n－1)3个．
练习册系列答案
走进文言文系列答案
相关题目
