题目内容
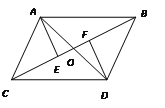
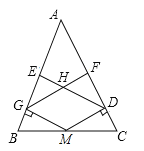
【题目】在△ABC中,AB=AC,BM=CM,MD⊥AC,MG⊥AB,DE⊥AB,GF⊥AC.求证:四边形HGMD是菱形.
【答案】证明见解析.
【解析】
连接AM,根据同一平面内垂直于同一条直线的两直线互相平行可证明MG∥DE,GF∥DM,进而可得四边形HGMD是平行四边形,再根据等腰三角形三线合一的性质可得AM平分∠BAC,再由角平分线的性质可得MG=MD,进而可得四边形HGMD是菱形.
连接AM,

∵MG⊥AB,DE⊥AB,
∴MG∥DE,
∵MD⊥AC,GF⊥AC,
∴GF∥DM,
∴四边形HGMD是平行四边形,
∵AB=AC,M为边BC的中点,
∴AM平分∠BAC,
∵MG⊥AB,MD⊥AC,
∴MG=MD,
∴四边形HGMD是菱形.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计.以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题: :
组别 | 分组 | 频数 | 频率 |
1 |
| 9 | 0.18 |
2 |
|
|
|
3 |
| 21 | 0.42 |
4 |
|
| 0.06 |
5 |
| 2 |
|

(1)根据上表填空: ![]() __,
__,![]() =. ,
=. ,![]() = .
= .
(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在![]() 的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?