题目内容
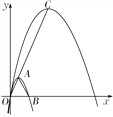
【题目】如图,抛物线C1:y=-![]() x2+2
x2+2![]() x的顶点为A,与x轴的正半轴交于点B.
x的顶点为A,与x轴的正半轴交于点B.
(1)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的表达式;
(2)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,抛物线C2的顶点为C,求抛物线C2的表达式(用k表示);
(3)在(2)条件下,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.当k>1时,求k的值.
【答案】(1)y=-![]() x2+2
x2+2![]() x;(2) y=-
x;(2) y=-![]() x2+2
x2+2![]() x;(3) k=
x;(3) k=![]()
【解析】(1)由抛物线C1解析式求出A、B及原点坐标,将三点坐标都扩大到原来的2倍,利用待定系数法求解可得;
(2)与(1)同理,利用待定系数法可得抛物线C2的解析式;
(3)求出顶点C的坐标,根据 S△PAC=S△ABC知BP∥AC,继而可得△ABO是边长为2的正三角形,四边形CEBP是矩形,表示出点P的坐标,将其代入到抛物线C2解析式可求得k的值.
解:(1)∵y=-![]() x2+2
x2+2![]() x=-
x=-![]() (x-1)2+
(x-1)2+![]() ,
,
∴抛物线C1经过原点O,点A(1,![]() )和点B(2,0)三点,
)和点B(2,0)三点,
∵将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,
∴变换后的抛物线经过原点O,(2,2![]() )和(4,0)三点.
)和(4,0)三点.
设变换后抛物线的表达式为y=ax2+bx,将(2,2![]() )和(4,0)代入,
)和(4,0)代入,
得![]() ,解得
,解得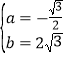 .
.
∴变换后抛物线的表达式为y=-![]() x2+2
x2+2![]() x;
x;
(2)∵抛物线C1经过原点O,点A(1,![]() )和点B(2,0)三点,
)和点B(2,0)三点,
将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,则抛物线C2过原点O,(k,![]() k),(2k,0)三点,
k),(2k,0)三点,
∴抛物线C2的表达式为y=-![]() x2+2
x2+2![]() x;
x;
(3)∵y=-![]() x2+2
x2+2![]() x=-
x=-![]() (x-k)2+
(x-k)2+![]() k,
k,
∴O,A,C三点共线,且顶点C为(k,![]() k).
k).
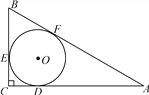
如答图,∵S△PAC=S△ABC,k>1,∴BP∥AC,
过点P作PD⊥x轴于D,过点B作BE⊥AO于E.
由题意知△ABO是边长为2的正三角形,四边形CEBP是矩形,
∴OE=1,CE=BP=2k-1,∵∠PBD=60°,
∴BD=k-![]() ,PD=
,PD=![]() (2k-1),
(2k-1),
∴P![]() ,
,
∴![]() (2k-1)=-
(2k-1)=-![]() ,解得k=
,解得k=![]() .
.