题目内容
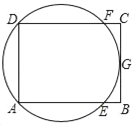
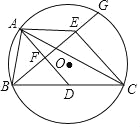
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)根据三角形中位线的性质和平行四边形的判定证明即可;
(2)根据平行四边形的性质和等腰三角形的性质解答即可.
(1)∵AD是△ABC的中线,
∴D是BC的中点,
∵F是BE的中点,
∴DF是△BCE的中位线,
∴DF∥CE,
∴AD∥CE,
∵AE∥BC,
∴四边形ADCE是平行四边形;
(2)∵四边形ADCE是平行四边形,
∴AE=CD,
∵AD是△ABC的中线,
∴BC=2CD,
∴BC=2AE,
∵BC=2AB,
∴AB=AE,
∴∠ABE=∠AEB,
∵AE∥BC,
∴∠AEB=∠DBE,
∴∠ABE=∠DBE,
∴![]() .
.

【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
【题目】在推进城乡生活垃圾分类的行动中,某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况,对![]() 两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
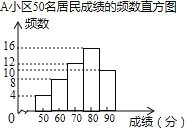
(信息二)上图中,从左往右第四组成绩如下:
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区600名居民成绩能超过平均数的人数;
小区600名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.