题目内容
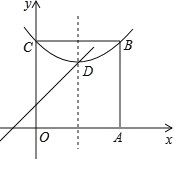
【题目】如图①,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 两点,且与y轴交于点C.
两点,且与y轴交于点C.

(1)求抛物线的表达式;
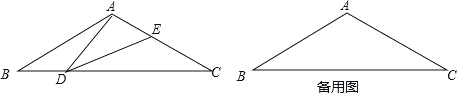
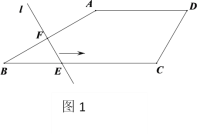
(2)如图①,在抛物线的对称轴上寻找一点M,使得△ACM的周长最小,求点M的坐标.
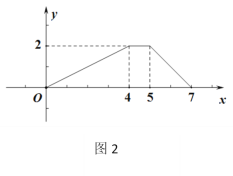
(3)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P,Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP,DQ.若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D的坐标;
,求△DPQ面积的最大值,并求此时点D的坐标;
【答案】(1)![]() ;(2)(1,2);(3)
;(2)(1,2);(3)![]() 的面积最大值为8,此时点
的面积最大值为8,此时点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
【解析】
(1)根据待定系数法求解即可;
(2)本题是典型的“将军饮马”问题,由抛物线的对称性知:点A关于对称轴的对称点为点B,故只需连接BC交直线x=1于点M,则M就是使得△ACM周长最小的点,然后根据待定系数法求出直线BC的解析式,而抛物线的对称轴易求,则点M的坐标可得;
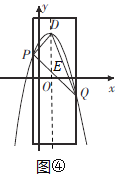
(3)根据题意易求出点P、Q两点坐标,然后利用待定系数法可求出直线PQ的解析式,过点![]() 作DE∥y轴交直线
作DE∥y轴交直线![]() 于点
于点![]() ,如图④,设点D的横坐标为x,则DE的长可用含x的代数式表示,再根据
,如图④,设点D的横坐标为x,则DE的长可用含x的代数式表示,再根据![]() 可得
可得![]() 关于x的关系式,然后根据二次函数的性质即可求出结果.
关于x的关系式,然后根据二次函数的性质即可求出结果.
解:(1)将![]() 、
、![]() 代入
代入![]() ,得:
,得:
![]() ,
,
解得:![]() ,
,
![]() 抛物线的表达式为
抛物线的表达式为![]() ;
;
(2)∵抛物线的解析式是![]() ,
,
当x=0时,y=3,
∴点C的坐标为(0,3),抛物线的对称轴为直线x=1,
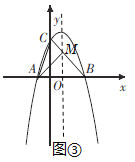
根据抛物线的对称性知:点A关于对称轴的对称点为点B,连接BC交直线x=1于点M,则M就是使得△ACM周长最小的点,如图③,
设直线BC的解析式为y=kx+3,
∵点B(3,0)在直线BC上,
∴0=3k+3,
解得:k=﹣1,
即直线BC的解析式为y=﹣x+3,
当x=1时,y=﹣1+3=2,
故BC与对称轴的交点M的坐标为(1,2),
∴△ACM周长最小时,点M的坐标为(1,2);
(3)当点![]() 的横坐标为
的横坐标为![]() 时,点
时,点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
设直线![]() 的表达式为
的表达式为![]() ,
,
将![]() ,
,![]() 、
、![]() ,
,![]() 代入
代入![]() ,得:
,得: ,
,
解得: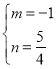 ,
,
![]() 直线
直线![]() 的表达式为
的表达式为![]() .
.
如图④,过点![]() 作DE∥y轴交直线
作DE∥y轴交直线![]() 于点
于点![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的面积取最大值,最大值为8,此时点
的面积取最大值,最大值为8,此时点![]() 的坐标为
的坐标为![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案