题目内容
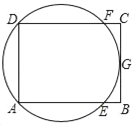
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法,其中正确说法的个数是( )
(1)AC与BD的交点是圆O的圆心;
(2)AF与DE的交点是圆O的圆心;
(3)![]() ;
;
(4)DE>DG,
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】
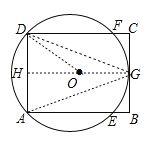
连接DG、AG,作GH⊥AD于H,连接OD,如图,先确定AG=DG,则![]() ;接着利用OG=OD可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心,根据圆周角定理得到DE是圆的直径,于是可判断DE>DG.
;接着利用OG=OD可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心,根据圆周角定理得到DE是圆的直径,于是可判断DE>DG.
连接DG、AG,作GH⊥AD于H,连接OD,如图,
∵G是BC的中点,
∴AG=DG,
∴![]() ;
;
∴HG⊥AD,
∵OG=OD,
∴点O不是HG的中点,
∴圆心O不是AC与BD的交点;
而四边形AEFD为⊙O的内接矩形,
∴AF与DE的交点是圆O的圆心;
∵∠DAB=90°,
∴DE是⊙的直径,
∴DE>DG,
∴(1)错误,(2)(3)(4)正确.
故选:D.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员.