��Ŀ����
����Ŀ��ʵ����̽���������������� 1��3��5��7�����г����µ���������ʮ�ֿ��� 5 ����(��ͼ)
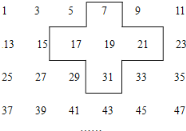
(1)����ʮ�ֿ���������ƽ�ƣ���һ��Ҫ��ס�����е� 5 �����������м����Ϊ a���� a �Ĵ���ʽ��ʾʮ�ֿ��ס�� 5 ������֮�ͣ�
(2)ʮ�ֿ��ס�� 5 ����֮���ܵ��� 285 �����ܣ��ֱ�д��ʮ�ֿ��ס�� 5 �����������ܣ���˵�����ɣ�
(3)ʮ�ֿ��ס�� 5 ����֮���ܵ��� 365 �����ܣ��ֱ�д��ʮ�ֿ��ס�� 5 �����������ܣ���˵�����ɣ�
���𰸡�(1) 5a���ƿ��ԣ�45��55��57��59��69���Dz����ܣ�
��������
��1���ӱ���ɿ��������������12�������������2���м����Ϊa�������Ϊa-12�������Ϊa+12�������Ϊa-2�������Ϊa+2����5�����ĺͿ���a����ʾ��
��2������285��������Ľ���������Ϳ��ԣ��ٿ����м�����λ�ã����ɵó��𰸣�
��3������365��������Ľ���������Ϳ��ԣ��ٿ����м�����λ�ã����ɵó��𰸣�
�⣺(1)�ӱ���֪���м����Ϊ a�������Ϊ a��12�������Ϊ a+12�������Ϊ a��2�������Ϊ a+2�� a+(a��2)+(a+2)+(a��12)+(a+12)=5a��
��5a=285��a=57��a=57 Ϊ�����ڵ� 5 �У����Կ��ԣ�
ʮ�ֿ��ס�� 5 �����ֱ�,45��55��57��59��69��.
��5a=365�� a=73��
����Ϊ 73��12=6.....1������ 73 �ڵ� 7 �е�һ�У�
��Ϊ������� a ��ʮ�ֿ����м�������ʲ����ܣ�

 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
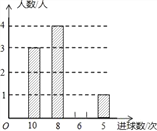
��У���˳�̾�ϵ�д�����Ŀ��ijУ���꼶ѧ����һ���������У�ѡһ��ѧ������Ͷ��������ÿ��Ͷ10�Σ�����Ͷ���������������ͳ�Ʒ��������������²�������ͳ�Ʊ���ͳ��ͼ��
���� | 10 | 8 | 6 | 5 |
���� | 3 | a | 2 | 1 |
��1������a=�� ����
��2���뽫����ͳ��ͼ����������
��3����С���Ա��ѡһ��ѧ���μ�У����Ͷ��������Ͷ��10��ij�Ա��ѡ�еĸ���Ϊ���٣�