题目内容
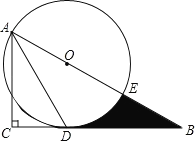
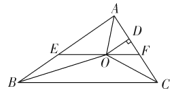
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .给出以下四个结论:
.给出以下四个结论:
①若![]() ,
,![]() ;
;
②![]() ;
;
③![]() 平分
平分![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的有________.(把所有正确结论的序号都选上)
【答案】②③④
【解析】
运用三角形内角和定理和角平分线的定义进行计算,即可判定①;根据平行线等分线段定理和角平分线定理即可确定②;根据三角形三条角平分线交于一点,即可判定③;设O到AE的距离为h,h=OD=3,然后求三角形AEF的面积即可判定④.
解:∵![]()
∴∠ABC+∠ACB=180°-80°=100°
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB) =50°
(∠ABC+∠ACB) =50°
∴![]() =180°-∠OBC+∠OCB=130°,故①错误;
=180°-∠OBC+∠OCB=130°,故①错误;
∵![]()
∴![]()
∵OB平分∠ABC
∴∠ABO=∠OBC
∵![]()
∴∠EOB=∠OBC
∴∠EOB=∠EBO
∴OE=BE,同理:CF=OF
∴![]() ,即②正确;
,即②正确;
∵![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]()
∴O为三个角的角平分线的交点,即![]() 平分
平分![]() ,故③正确;
,故③正确;
设O到AE的距离为h,即高为h
∵O为三个角的角平分线的交点
∴h=CD=3
∴S△AEF= S△AOE+ S△AOF=![]() ×AE·h+
×AE·h+![]() ×AF·CD=
×AF·CD=![]() ×3(AE+AF)
×3(AE+AF)
∵AE+AF=8
∴S△AEF=12,故④正确;
故答案为②③④.

 名校课堂系列答案
名校课堂系列答案【题目】中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.
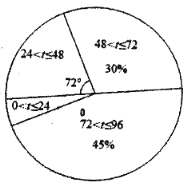
去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图
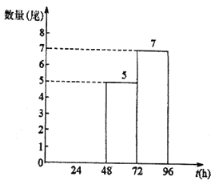
今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 | 中位数 | 众数 | 方差 | |
去年 | 64.2 | 68 | 73 | 715.6 |
今年 | 56.2 | a | 68 | 629.7 |
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.