题目内容
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．
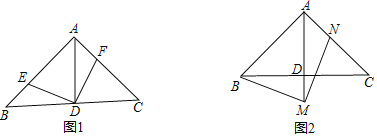
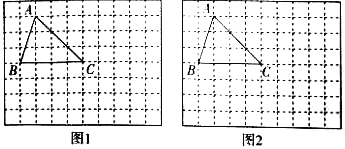
（1）如图1，点E，F在AB，AC上，且∠EDF=90°．求证：BE=AF；
（2）点M，N分别在直线AD，AC上，且∠BMN=90°．如图2，当点M在AD的延长线上时，求证：AB+AN=
AM；
【答案】（1）见解析；（2）见解析
【解析】
（1）先证∠BDE=∠ADF，再证△BDE≌△ADF，即可证明BE=AF；
（2）过点M作MP⊥AM，交AB的延长线于点P，先证△AMN≌△PMB，在Rt△AMP中，即可证明AB+AN=
AM.
解：（1）∵∠BAC=90°，AB=AC，
∴∠B=∠C=45°，
∵AD⊥BC，
∴BD=CD，∠BAD=∠CAD=45°，
∴∠CAD=∠B，AD=BD，
∵∠EDF=∠ADC=90°，
∴∠BDE=∠ADF，
在△BDE和△ADF中
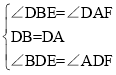
∴△BDE≌△ADF（ASA），
∴DE=DF；
（2）如图，过点M作MP⊥AM，交AB的延长线于点P，
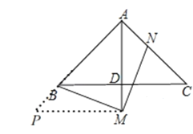
∴∠AMP=90°．
∵∠PAM=45°，
∴∠P=∠PAM=45°，
∴AM=PM．
∵∠BMN=∠AMP=90°，
∴∠BMP=∠AMN．
∵∠DAC=∠P=45°，
在△AMN和△PMB
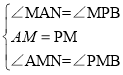
∴△AMN≌△PMB（ASA），
∴AN=PB，
∴AP=AB+BP=AB+AN，
在Rt△AMP中，∠AMP=90°，AM=MP，
∴AP=AM，
∴AB+AN=AM.
【题目】调查作业：了解你所住小区家庭3月份用气量情况．
小天、小东和小芸三位同学住在同一小区，该小区共有300户家庭，每户家庭人数在2—5之间，这300户家庭的平均人数约为3.3．
小天、小东和小芸各自对该小区家庭3月份用气量情况进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2、表3，
表1抽样调查小区4户家庭3月份用气量统计表（单位：
）
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表（单位：）
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表（单位：）
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题：
（1）小天、小东和小芸三人中，哪一位同学抽样调查的数据能较好地反应出该小区家庭3月份用气量情况？请简要说明其他两位同学抽样调查的不足之处；
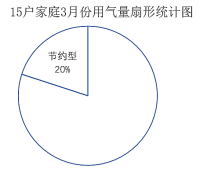
（2）小东将表2中的数据按用气量
大小分为三类；
①节约型：
；
②居中型：
；
③偏高型：
；并绘制成如下扇形统计图，请帮助他将扇形图补充完整；
（3）小芸算出表3中3月份平均每人的用量为
，请估计该小区3月份的总用气量．
