题目内容
【题目】直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
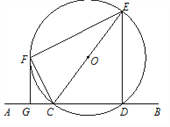
(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
【答案】(1)证明见解析(2)48
【解析】试题分析:(1)利用角平分线的性质以及等腰三角形的性质得出∠OFC=∠FCG,继而得出∠GFC+∠OFC=90°,即可得出答案;
(2)首先得出四边形FGDH是矩形,进而利用勾股定理得出HO的长,进而得出答案.
试题解析:(1)连接FO,
∵ OF=OC,
∴ ∠OFC=∠OCF.
∵CF平分∠ACE,
∴∠FCG=∠FCE.
∴∠OFC=∠FCG.
∵ CE是⊙O的直径,
∴∠EDG=90°,
又∵FG∥ED,
∴∠FGC=180°-∠EDG=90°,
∴∠GFC+∠FCG=90°
∴∠GFC+∠OFC=90°,
即∠GFO=90°,
∴OF⊥GF,
又∵OF是⊙O半径,
∴FG与⊙O相切.
(2)延长FO,与ED交于点H,
由(1)可知∠HFG=∠FGD=∠GDH=90°,
∴四边形FGDH是矩形.
∴FH⊥ED,
∴HE=HD.
又∵四边形FGDH是矩形,FG=HD,
∴HE=FG=4.
∴ED=8.
∵在Rt△OHE中,∠OHE=90°,
∴OH=OE2-HE2=52-42=3.
∴FH=FO+OH=5+3=8.
S四边形FGDH=12(FG+ED)FH=12×(4+8)×8=48.

练习册系列答案
相关题目