Question

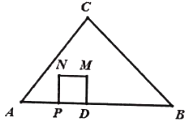
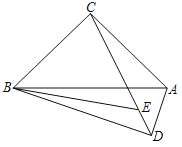
【题目】如图，等腰直角△ABC的斜边AB下方有一动点D，∠ADB＝90°，BE平分∠ABD交CD于点E，则的最小值是_____．

Answer 1

【答案】

【解析】

如图，取AB的中点O，连接OC，OD，AE．想办法证明CE=CA，当CD是直径时的值最小．

如图，取AB的中点O，连接OC，OD，AE．

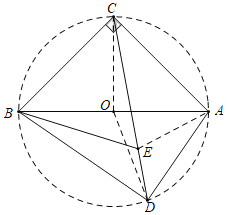
∵∠ACB＝∠ADB＝90°，OA＝OB，

∴OC＝OD＝AB，

∴A，C，B，D四点共圆，

∵CA＝CB，

∴∠CBA＝∠CBA＝45°，

∴∠CDA＝∠CBA＝45°，∠CDB＝∠CAB＝45°，

∴∠CDB＝∠CDA，

∵BE平分∠ABD，

∴AE平分∠BAD，

∴∠BAE＝∠DAE，

∵∠CAE＝∠CAB+∠BAE＝45°+∠BAE，∠CEA＝∠EDA+∠EAD＝45°+∠DAE，

∴∠CAE＝∠CEA，

∴CA＝CE＝定值，

∴当CD的值最大时，的值最小，

∴CD是直径时，的值最小，最小值＝＝，

故答案为．