题目内容
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.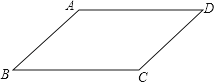
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
【答案】
(1)
BC=DA
(2)
证明:连接AC,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC,
在△ABC和△CDA中, 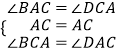 ,
,
∴△ABC≌△CDA(ASA),
∴AB=CD,BC=DA;
故答案为:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC,
在△ABC和△CDA中, 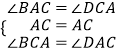 ,
,
∴△ABC≌△CDA(ASA),
∴AB=CD,BC=DA.
【解析】(1)已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
故答案为:BC=DA;
本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形对边平行的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目