题目内容
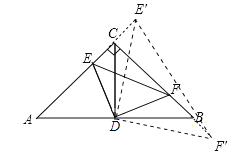
【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

【答案】![]() 或
或![]()
【解析】解:①E在线段AC上.在△ADE和△CDF中,∵AD=CD,∠A=∠DCF,AE=CF,∴△ADE≌△CDF(SAS),∴同理△CDE≌△BDF,∴四边形CEDF面积是△ABC面积的一半.∵CE=1,∴CF=4﹣1=3,∴△CEF的面积=![]() CECF=
CECF=![]() ,∴△DEF的面积=
,∴△DEF的面积=![]() ×
×![]() ×
×![]() ﹣
﹣![]() =
=![]() .
.
②E'在AC延长线上.∵AE'=CF',AC=BC=4,∠ACB=90°,∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=![]() ,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CDCE'cos135°=1+8+2×
,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CDCE'cos135°=1+8+2×![]() ×
×![]() =13,∴S△E'DF'=
=13,∴S△E'DF'=![]() DE'2=
DE'2=![]() .故答案为:
.故答案为: ![]() 或
或![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目