题目内容
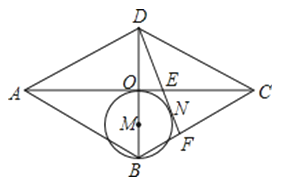
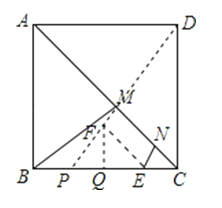
【题目】如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为![]() 的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是 .
的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是 . 
【答案】![]()
【解析】解:作EF∥AC且EF=![]() , 连结DF交AC于M,在AC上截取MN=
, 连结DF交AC于M,在AC上截取MN=![]() , 延长DF交BC于P,作FQ⊥BC于Q,
, 延长DF交BC于P,作FQ⊥BC于Q,
则四边形BMNE的周长最小,
由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,
∵∠DPC=∠FPQ,∠DCP=∠FQP,
∴△PFQ∽△PDC,
∴ ![]() =
=![]() ,
,
∴ ![]() =
=![]() ,
,
解得:PQ=![]() ,
,
∴PC=![]() ,
,
由对称性可求得tan∠MBC=tan∠PDC=![]() =
=![]() .
.
所以答案是![]() .
. 
【考点精析】认真审题,首先需要了解轴对称-最短路线问题(已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目