题目内容
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )

| A.(0,0) | B.(0,1) | C.(0,2) | D.(0,3) |

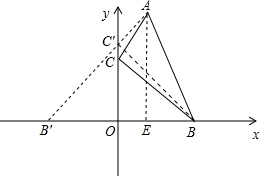
作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(3,0),
∴B′点坐标为:(-3,0),AE=4,
则B′E=4,即B′E=AE,
∵C′O∥AE,
∴B′O=C′O=3,
∴点C′的坐标是(0,3),此时△ABC的周长最小.
故选:D.
此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(3,0),
∴B′点坐标为:(-3,0),AE=4,
则B′E=4,即B′E=AE,
∵C′O∥AE,
∴B′O=C′O=3,
∴点C′的坐标是(0,3),此时△ABC的周长最小.
故选:D.


练习册系列答案
相关题目