Question

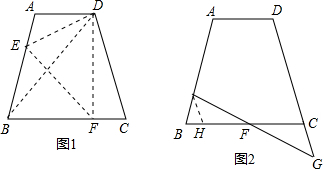
如图，已知∠AOB=25°，把∠AOB绕顶点O按逆时针旋转55°到∠MON，点C、D分别是OB、OM上的点，分别作C点关于OA、ON的对称点E、F，连接DE、DF．
（1）求∠ECF的度数；
（2）说明DE=DF的理由．

Answer 1

（1）∵C点关于OA、ON的对称点分别为E、F，
∴OA、ON分别是EC、CF的垂直平分线，
∵∠AON=55°+25°=80°，
∴∠OCE=90°-∠COA=65°，∠OCF=90°-∠BON=10°，
∴∠ECF=∠OCE+∠OCF=75°．

（2）连接OE、OF，
由（1）知，OA、ON分别是EC、CF的垂直平分线，
∴OE=OC=OF，
由对称性知：∠E0A=∠AOB=25°∠NOF=∠NOB=55°，
∴∠E0D=∠FOD=80°，
在△OED与△OFD中

OE=OF ∠EOD=∠FOD OD=OD

，
∴△OED≌△OFD（SAS），
∴DE=DF．