题目内容
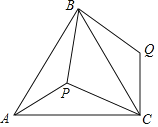
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
【答案】(1)6;(2)150°
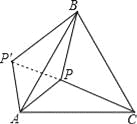
【解析】试题分析:先根据等边三角形的性质得AB=AC,∠BAC=60°,再利用旋转的性质得∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,于是可判断△AP′P为等边三角形,得到PP′=AP=5,∠APP′=60°,接着根据勾股定理的逆定理证明△BPP′为直角三角形,且∠BPP′=90°,然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数.
试题解析:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.

【题目】某公司为了更好治理污水质,改善环境,决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 200 | 160 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少1万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过78万元,你认为该公司有哪几种购买方案;
(3)在(2)间的条件下,若每月要求处理的污水量不低于1620吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.