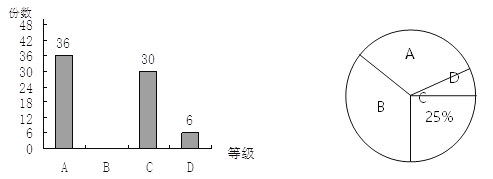
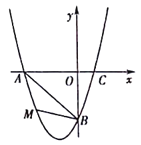
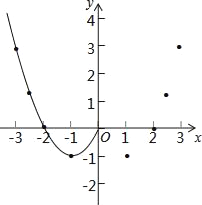题目内容
【题目】如图所示，直线AB、CD相交于点O，OM⊥AB．
(1)若∠1＝∠2，判断ON与CD的位置关系，并说明理由；
(2)若∠1＝
∠BOC，求∠MOD的度数．
【答案】（1）ON⊥CD，理由见解析；（2）157.5°
【解析】
（1）根据垂直的定义可得∠AOM=90°，进而可得∠1+∠AOC=90°，再利用等量代换可得∠2+∠AOC=90°，从而可得ON⊥CD．
（2）由题意可得∠1=
∠BOC=(∠1+90°) ，进而可得∠MOD＝90°+∠BOD=90°+∠AOC=180°－∠1，再代入∠1的度数即可的解.
(1)ON⊥CD.理由如下：
∵OM⊥AB，∴∠AOM=90°，
∴∠1+∠AOC=90°，
又∵∠1=∠2，∴∠2+∠AOC=90°，
即∠CON=90°，∴ON⊥CD．
(2) ∠1=∠BOC=(∠1+90°) ，
∵∠1=22.5°，∴ ∠MOD＝90°+∠BOD=90°+∠AOC=180°－∠1= 157.5°
练习册系列答案
相关题目
【题目】在数学拓展课上，九（1）班同学根据学习函数的经验，对新函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下：
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标；
【类比探究】当函数y=x2﹣2|x|时，自变量x的取值范围是全体实数，下表为y与x的几组对应值．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分；
②根据画出的函数图象，写出该函数的两条性质．
【深入探究】若点M（m，y1）在图象上，且y1≤0，若点N（m+k，y2）也在图象上，且满足y2≥3恒成立，求k的取值范围．
