题目内容
【题目】某校组织了“健康教育”手抄报征集活动,现从中抽取部分作品,按A、B、C、D四个等级进行奖励,并根据统计结果绘制了如下两幅不完整统计图.
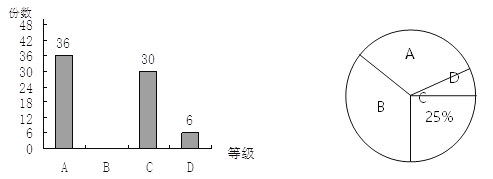
(1)求抽取了多少份作品.
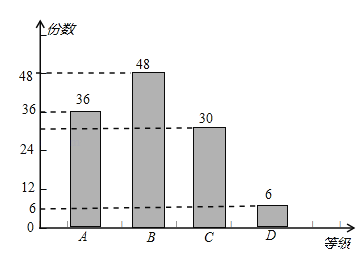
(2)被抽取作品中B等级有多少份?并补全条形统计图.
(3)扇形统计图中D等级所对的圆心角是多少度?
(4)若全校共征集到作品600份,请估计A作品有多少份?
【答案】(1)120(份);(2)48(份),详见解析;(3)18°;(4)180份.
【解析】
(1)用C等级份数除以C等级所占的百分比,可得抽取的数量;
(2)用(1)中所求总份数减去A、C、D三等级数量即可得到B等级作品数,并补全统计图;
(3)先算出D等级所占总数的百分比,再乘以360°,即可算出度数.
(4)利用样本估计总体,将样本中A等级所占比例乘以600,可估计A等级数量.
(1)根据题意,共抽取作品30÷25%=120(份);
(2)B等级作品数为:120﹣36﹣30﹣6=48(份),
补全条形统计图如图所示:
(3)6÷120=5%,360°×5%=18°.
(4)600×![]() =180,
=180,
答:若该校共征集到600份作品,估计等级为A的作品约有180份.

【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.