Question

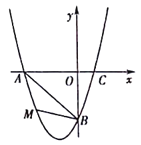
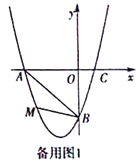
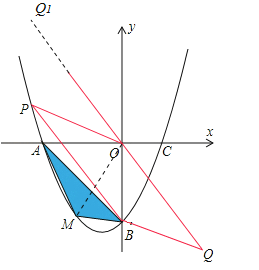
【题目】在平面直角坐标系中，已知抛物线经过A(－3，0)，B(0，－3)，C(1，0)三点.

(1)求抛物线的解析式；

(2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S.求S

关于m的函数关系式，并求出S的最大值；

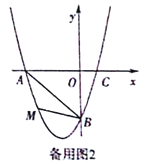
(3)若点P是抛物线上的动点，点Q是直线y=－x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标.

Answer 1

【答案】（1）

时，S最大为

（3）（－3，3）或或或（3，－3）

【解析】试题分析：（1）先假设出函数解析式，利用三点法求解函数解析式．

（2）设出M点的坐标，利用S=S△AOM+S△OBM﹣S△AOB即可进行解答；

（3）当OB是平行四边形的边时，表示出PQ的长，再根据平行四边形的对边相等列出方程求解即可；当OB是对角线时，由图可知点A与P应该重合，即可得出结论．

试题解析：解：（1）设此抛物线的函数解析式为：y=ax2+bx+c（a≠0），

将A（－3，0），B（0，－3），C（1，0）三点代入函数解析式得：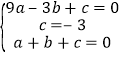

解得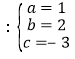，所以此函数解析式为：．

（2）∵M点的横坐标为m，且点M在这条抛物线上，∴M点的坐标为：（m，），

∴S=S△AOM+S△OBM-S△AOB=×3×（-）+×3×（-m）-×3×3=-（m+）2+，

当m=-时，S有最大值为：S=-．

（3）设P（x，）．分两种情况讨论：

①当OB为边时，根据平行四边形的性质知PB∥OQ，

∴Q的横坐标的绝对值等于P的横坐标的绝对值，

又∵直线的解析式为y=-x，则Q（x，-x）．

PQ=OB，得：|-x-（）|=3

解得： x=0（不合题意，舍去），-3， ，∴Q的坐标为（－3，3）或或；

②当BO为对角线时，如图，知A与P应该重合，OP=3．四边形PBQO为平行四边形则BQ=OP=3，Q横坐标为3，代入y=﹣x得出Q为（3，﹣3）．

综上所述：Q的坐标为：（－3，3）或或或（3，－3）．