题目内容
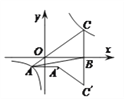
【题目】如图，在一笔直的海岸线l上有A、B两个观测站，C离海岸线l的距离(即CD的长)为2，从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则AB的长( )
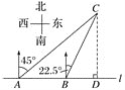
A. 2 km B. (2＋
)km C. (4－2) km D. (4－) km
【答案】C
【解析】
根据题意在CD上取一点E，使BD=DE，设AB=x，则DE=2-x，EC=
（2-x），再根据DE+EC=CD列出方程2-x+（2-x）=2，求解即可．
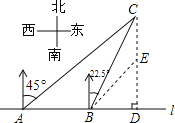
解：在CD上取一点E，使BD=DE，
可得：∠EBD=∠BED =45°，
∵从A测得船C在北偏东45°的方向，
∴AD=DC=2，
∵从B测得船C在北偏东22.5°的方向，
∴∠BCE=∠CBE=22.5°，
∴BE=EC．
设AB=x，则DE=BD=AD-AB=2-x，
∴EC=BE=BD=（2-x），
∵DE+EC=CD，
∴2-x+（2-x）=2，
解得x=4-2，即AB=4-2．
故选：C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
