题目内容
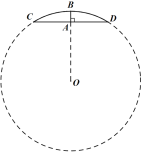
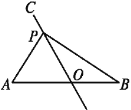
【题目】如图,⊙O的半径OA⊥弦BC于H,D是⊙O上另一点,AD与BC相交于点E,若DC=DE,OB=![]() ,AB=5.
,AB=5.
(1)求证:∠AOB=2∠ADC.
(2)求AE长.
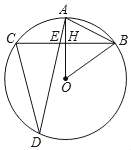
【答案】(1)详见解析;(2)AE=![]()
【解析】
(1)根据垂径定理可得![]() ,可得∠AOC=∠AOB,根据圆周角定理可得∠AOB=2∠ADC;
,可得∠AOC=∠AOB,根据圆周角定理可得∠AOB=2∠ADC;
(2)由题意可证AB=BE=5,根据勾股定理可求AH=3,即可求EH的长,根据勾股定理可得AE的长.
证明:(1)如图,连接OC,
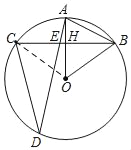
∵OA⊥BC,
∴![]() ,
,
∴∠AOC=∠AOB,
∵∠AOC=2∠ADC,
∴∠AOB=2∠ADC
(2)∵DC=DE
∴∠DCE=∠DEC
∵∠DCE=∠DAB,∠DEC=∠AEB,
∴∠AEB=∠DAB,
∴AB=BE=5
∵AH2+BH2=AB2,OH2+BH2=OB2,
∴AB2﹣AH2=BH2=OB2﹣(AO﹣AH)2,
∴![]() ,
,
∴AH=3,
∴BH=4,
∴EH=BE﹣BH=1,
∴AE=![]() =
=![]()

练习册系列答案
相关题目