Question

【题目】如图，中，，，与相切于点，求图中阴影部分的面积.（结果保留）

Answer 1

【答案】4-

【解析】

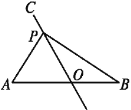
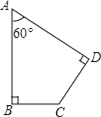
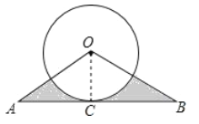
由AB为圆的切线，得到OC⊥AB，再由OA=OB，利用三线合一得到C为AB中点，且OC为角平分线，在直角三角形AOC中，利用30度所对的直角边等于斜边的一半求出OC的长，利用勾股定理求出AC的长，进而确定出AB的长，求出∠AOB度数，阴影部分面积=三角形AOB面积-扇形AOB面积，求出即可．

连接OC，

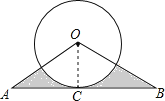
∵AB与圆O相切，

∴OC⊥AB，

∵OA=OB，

∴∠AOC=∠BOC，∠A=∠B=30°，

在Rt△AOC中，∠A=30°，OA=4，

∴OC=OA=2，∠AOC=60°，

∴∠AOB=120°，AC==2，即AB=2AC=4，

则S阴影=S△AOB-S扇形=×4×2-=4-．

故图中阴影部分的面积为4-．