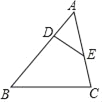
题目内容
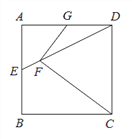
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点.
边上的动点.
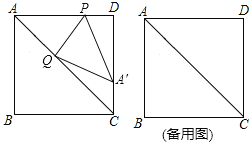
(1)AC等于多少;
(2)若![]() ,且点
,且点![]() 关于
关于![]() 的对称点
的对称点![]() 落在
落在![]() 边上,求
边上,求![]() 的值;
的值;
(3)设![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 与
与![]() 面积之和
面积之和![]() 的最小值.(用含
的最小值.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 与
与![]() 面积之和
面积之和![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)由正方形的性质可得对角线的长,
(2)由点A与点A′关于PQ对称知△APQ与△A′PQ关于PQ对称,再证∠PA′D=∠A′QC,由AB=4,AP=3PD得PD=1,AP=PA′=3,A′D=2![]() ,利用正切函数的定义即可得答案,
,利用正切函数的定义即可得答案,
(3)过点Q作直线MN⊥AD于点M,交BC于点N,则MN⊥BC,证△APQ∽△CTQ得![]() =
=![]() ,设QM=h,则QN=4-h,CT=
,设QM=h,则QN=4-h,CT=![]() ,继而知S=
,继而知S=![]() ah+
ah+![]()
![]() (4-h),整理得ah2-(4a+S)h+8a=0,根据方程有实数根得(4a+S)2≥32a2,结合4a+S>0知S≥(4
(4-h),整理得ah2-(4a+S)h+8a=0,根据方程有实数根得(4a+S)2≥32a2,结合4a+S>0知S≥(4![]() -4)a,最后根据S=(4
-4)a,最后根据S=(4![]() -4)a时可得h=2
-4)a时可得h=2![]() .
.
解:(1)∵四边形ABCD是正方形,且AB=4,
∴AB=BC=4,∠BAC=∠ACB=45°,
∴AC=![]() =
=![]() =
=![]() ,
,
(2)如图1,
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
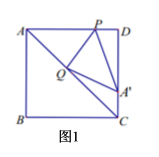
(3)如图2,过点![]() 作直线
作直线![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
∵关于![]() 的一元二次方程
的一元二次方程![]() 有实根,∴
有实根,∴![]() ,
,
∴![]() ,
,
![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,由方程
时,由方程![]() 可得
可得![]() 满足题意,
满足题意,
故当![]() 时,
时,![]() 与
与![]() 面积之和
面积之和![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
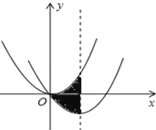
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()