题目内容
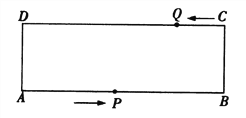
【题目】如图，在矩形ABCD中，AB=24 cm, BC=8 cm，点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动，点Q从点C开始沿CD边以2 cm/s的速度移动，如果点P，Q分别从点A，C同时出发，当其中一点到达点D时，另一点也随之停止运动，设运动时间为ts.当t为何值时，四边形QPBC为矩形?
【答案】4.
【解析】试题分析：求出CQ=2t，AP=4t，BP=24-4t，由已知推出∠B=∠C=90°，CD∥AB，推出CQ=BP时，四边形QPBC是矩形，得出方程2t=24-4t，求出即可．
试题解析：根据题意得：CQ=2t，AP=4t，
则BP=24-4t，
∵四边形ABCD是矩形，
∴∠B=∠C=90°，CD∥AB，
∴只有CQ=BP时，四边形QPBC是矩形，
即2t=24-4t，
解得：t=4，
答：当t=4s时，四边形QPBC是矩形．
练习册系列答案
相关题目
