题目内容
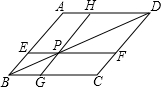 如图,在菱形ABCD中,过对角线BD上任一点P,作EF∥BC,GH∥AB,下列结论正确的是
如图,在菱形ABCD中,过对角线BD上任一点P,作EF∥BC,GH∥AB,下列结论正确的是①图中共有3个菱形;
②△BEP≌△BGP;
③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
分析:根据菱形的判定判断①即可;根据菱形性质求出四边形BEPG是平行四边形,推出PE=BG,PG=BE,根据全等三角形的判定推出△BEP≌△PGB,即可判断②;根据三角形面积公式即可判断③;求出四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,推出AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,求出AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,即可判断④.
同理AE=HP=DF=PF=CG,即可判断④.
解答:解:∵图中有三个菱形,如菱形ABCD、菱形HOFD、菱形BEPG,∴①正确;
∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,∠ABD=∠CBD,
∵EF∥BC,GH∥AB,
∴四边形BEPG是平行四边形,
∴PE=BG,PG=BE,
在△BEP和△PGB中,
∴△BEP≌△PGB(SSS),
∴②正确;
∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF∥BC,AB∥GH∥CD,
∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,
∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,
∵四边形ABCD是菱形,
∴∠EBP=∠GBP,
∵PE∥BG,
∴∠EPB=∠GBP,
∴∠EBP=∠EPB,
∴BE=PE,
∴AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,
∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;
故答案为:①②④.
∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,∠ABD=∠CBD,
∵EF∥BC,GH∥AB,
∴四边形BEPG是平行四边形,
∴PE=BG,PG=BE,
在△BEP和△PGB中,
|
∴△BEP≌△PGB(SSS),
∴②正确;
∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF∥BC,AB∥GH∥CD,
∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,
∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,
∵四边形ABCD是菱形,
∴∠EBP=∠GBP,
∵PE∥BG,
∴∠EPB=∠GBP,
∴∠EBP=∠EPB,
∴BE=PE,
∴AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,
∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;
故答案为:①②④.
点评:本题考查了菱形的性质和判定,平行四边形的性质和判定,全等三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,但是比较容易出错.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
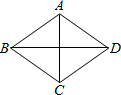 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
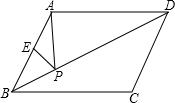
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.