题目内容
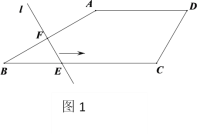
【题目】如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直线
,直线![]() .当直线
.当直线![]() 沿射线
沿射线![]() 方向,从点
方向,从点![]() 开始向右平移时,直线
开始向右平移时,直线![]() 与四边形
与四边形![]() 的边分别相交于点
的边分别相交于点![]() 、
、![]() .设直线
.设直线![]() 向右平移的距离为
向右平移的距离为![]() ,线段
,线段![]() 的长为
的长为![]() ,且
,且![]() 与
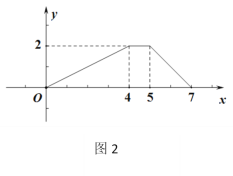
与![]() 的函数关系如图2所示,则四边形
的函数关系如图2所示,则四边形![]() 的周长是_____.
的周长是_____.
【答案】![]()
【解析】
根据图1直线l的平移过程分为三段,当F与A重合之前,x与y都不断增大,当当F与A重合之后到点E与点C重合之前,x增加y不变,E与点C重合后继续运动至F与D重合x增加y减小.结合图2可知BC=5,AD=7-4=3,由![]() 且∠B=30°可知AB=
且∠B=30°可知AB=![]() ,当F与A重合时,把CD平移到E点位置可得三角形AED′为正三角形,可得CD=2,进而可求得周长.
,当F与A重合时,把CD平移到E点位置可得三角形AED′为正三角形,可得CD=2,进而可求得周长.
由题意和图像易知BC=5,AD=7-4=3
当BE=4时(即F与A重合),EF=2
又∵![]() 且∠B=30°
且∠B=30°
∴AB=![]() ,
,
∵当F与A重合时,把CD平移到E点位置可得三角形AED′为正三角形
∴CD=2
∴AB+BC+CD+AD=![]() +5+2+3=10+
+5+2+3=10+![]()
故答案时![]() .
.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)