Question

【题目】如图，在平面直角坐标系中，真线与轴，轴分别交于、两点，为等腰直角三角形，且.若点恰好落在函数（）在第二象限内的图象上，则的值为（ ）

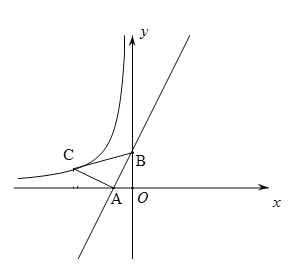
A.-1B.-2C.-3D.-4

Answer 1

【答案】C

【解析】

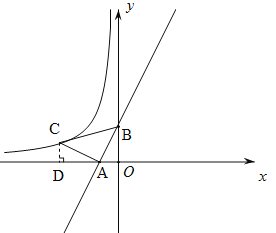
过点C作CD⊥x轴于点D，得出△AOB≌△CDA(AAS)，进而得出OD，CD的长，即可得出答案．

过点C作CD⊥x轴于点D．

∵直线y=2x+2与x轴、y轴分别交于A、B两点，

∴x=0时，y=2；y=0时，x=－1，

则AO=1，OB=2．

∵△BAC为等腰直角三角形，且∠BAC=90°，

∴AB=AC，∠OAB+∠DAC=90°．

∵∠ACD+∠CAD=90°，

∴∠OAB=∠ACD．

在△AOB和△CDA中，

∵，

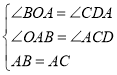∴△AOB≌△CDA(AAS)，

∴AO=CD=1，OB=AD=2，

∴OD=3，CD=1，

∴C(－3，1)，

∴k=－3×1=－3．

故选：C．