题目内容
(2013•徐汇区二模)在Rt△ABC中,∠C=90°,sinA=
,将△ABC绕点A旋转后,点C落在射线BA上,点B落到点D处,那么sin∠ADB的值等于
或
或
.
| 4 |
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
分析:作出图形,设BC=4a,AB=5a,求出AC,再根据旋转的性质可得AB=AD,AC=AC′,BC=C′D,然后分①逆时针旋转时,求出BC′,再利用勾股定理列式求出BD,根据等边对等角求出∠ADB=∠ABD,然后根据锐角的正弦等于对边比斜边列式计算即可得解;②顺时针旋转时,求出BC′,再利用勾股定理列式求出BD,过点A作AE⊥BD于E,根据等腰三角形三线合一的性质求出BE,再利用勾股定理列式求出AE,然后根据锐角的正弦值等于对边比斜边列式计算即可得解.
解答: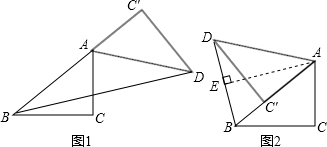 解:∵∠C=90°,sinA=
解:∵∠C=90°,sinA=
,
∴设BC=4a,AB=5a,
则AC=
=3a,
根据旋转的性质,AB=AD=5a,AC=AC′=3a,BC=C′D=4a,
①如图1,逆时针旋转时,BC′=AB+AC′=5a+3a=8a,
根据勾股定理,BD=
=
=4
a,
∵AB=AD,
∴∠ADB=∠ABD,
∴sin∠ADB=sin∠ABD=
=
=
;
②如图2,顺时针旋转时,BC′=AB-AC′=5-3=2,
根据勾股定理,BD=
=
=2
a,
过点A作AE⊥BD于E,则BE=
BD=
×2
a=
a,
在Rt△ABE中,AE=
=
=2
a,
∴sin∠ADB=
=
=
;
综上所述,sin∠ADB的值为
或
.
故答案为:
或
.
 解:∵∠C=90°,sinA=
解:∵∠C=90°,sinA=| 4 |
| 5 |
∴设BC=4a,AB=5a,
则AC=
| (5a)2-(4a)2 |
根据旋转的性质,AB=AD=5a,AC=AC′=3a,BC=C′D=4a,
①如图1,逆时针旋转时,BC′=AB+AC′=5a+3a=8a,
根据勾股定理,BD=
| BC′2+C′D2 |
| (8a)2+(4a)2 |
| 5 |
∵AB=AD,
∴∠ADB=∠ABD,
∴sin∠ADB=sin∠ABD=
| C′D |
| BD |
| 4a | ||
4
|
| ||
| 5 |
②如图2,顺时针旋转时,BC′=AB-AC′=5-3=2,
根据勾股定理,BD=
| BC′2+C′D2 |
| (2a)2+(4a)2 |
| 5 |
过点A作AE⊥BD于E,则BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
在Rt△ABE中,AE=
| AB2-BE2 |
(5a)2-(
|
| 5 |
∴sin∠ADB=
| AE |
| AD |
2
| ||
| 5a |
2
| ||
| 5 |
综上所述,sin∠ADB的值为
| ||
| 5 |
2
| ||
| 5 |
故答案为:
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查了旋转的性质,勾股定理的应用,等边对等角的性质,等腰三角形三线合一的性质,难点在于要分情况讨论并找出∠ADB所在的直角三角形,作出图形更形象直观.

练习册系列答案
相关题目