题目内容
如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
⑴求证:DC=BC;
⑵E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
(1)过A作DC的垂线AM交DC于M,
则
AM=BC=2.(1分) 又tan∠ADC=2,所以 .(2分)
.(2分)
因为MC=AB=1,所以DC=DM+MC=2,即DC=BC.(3分)
(2)等腰直角三角形.(4分)
证明:因为DE=DF,∠EDC=∠FBC,DC=BC. 所以,△DEC≌△BFC(5分)
所以,CE=CF,∠ECD=∠BCF.
所以,∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=90°
即△ECF是等腰直角三角形.(6分)
(3)设BE=k,则CE=CF=2k,所以 .(7分)
.(7分)
因为∠BEC=135°,又∠CEF=45°,所以∠BEF=90°.(8分)
所以 (9分)
(9分)
所以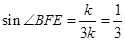 .(10分)
.(10分)
解析

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=