题目内容
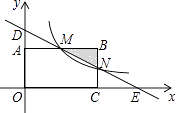
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( ) 
A.8S
B.9S
C.10S
D.11S
【答案】B
【解析】解:如图所示, ∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴S△DEF:S△BCF=( ![]() )2 ,
)2 ,
又∵E是AD中点,
∴DE= ![]() AD=
AD= ![]() BC,
BC,
∴DE:BC=DF:BF=1:2,
∴S△DEF:S△BCF=1:4,
∴S△BCF=4S,
又∵DF:BF=1:2,
∴S△DCF=2S,
∴SABCD=2(S△DCF+S△BCF)=12S.
∴四边形ABCE的面积=9S,
故选B.
【考点精析】本题主要考查了平行四边形的性质和相似三角形的判定与性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目
【题目】某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?