��Ŀ����
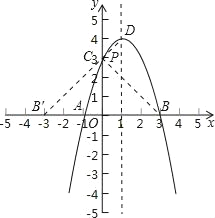
����Ŀ����֪������y=ax2+bx+c��a��0����x�ύ�ڲ�ͬ��������A��x1��0���͵�B��x2��0����y��������ύ�ڵ�C�����x1��x2�Ƿ���x2��2x��3=0����������x1��x2������ͼ���㣨2��3��
��1���������ߵĽ���ʽ������ͼ��
��2��x��ʲô��Χ�ں���ֵy����3����x�����������
��3���裨1���е������߶���ΪD����y�����Ƿ���ڵ�P��ʹ��DP+BP�ĺ���С�������ڣ���������Сֵ���������ڣ�˵�����ɣ�

���𰸡���1��y=��x2+2x+3����2��0��x��1����3��P������Ϊ��0��3����
���������������: ��1�����ݶ��κ�����һԪ���η��̵Ĺ�ϵ��֪������![]() ����������Ϊ������
����������Ϊ������![]() ��Ľ�������꣬���ô���ϵ�����г���������ʽ����
��Ľ�������꣬���ô���ϵ�����г���������ʽ����![]() �������ʽ�����ϵ�����ɣ����ݺ�������ʽ�������ͼ��Ķ������꣬�������������Ľ������꼴�ɻ�������ͼ��
�������ʽ�����ϵ�����ɣ����ݺ�������ʽ�������ͼ��Ķ������꣬�������������Ľ������꼴�ɻ�������ͼ��
��2������ͼ��ֱ�ӽ�ɣ�
��3����![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ��
��![]() ����Ϊ
����Ϊ![]() ����
����![]() ����
����![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() �����������ʽ����
�����������ʽ����![]() �ύ�����꼴Ϊ
�ύ�����꼴Ϊ![]() �����꣮
�����꣮
�����������1���躯������ʽΪ![]()
�ѵ㣨2��3������![]() �ã�
�ã� ![]()
���![]()
�ʺ�������ʽΪ![]()
��![]() ʱ��
ʱ�� ![]()
���![]()
�ʺ�����x��Ľ�������Ϊ![]() �͵�
�͵�![]()
��![]() ʱ��
ʱ�� ![]() ��������
��������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]()
����Ϊ����ͼ��Գ���Ϊ![]()
��![]() �������ʽ�ã�
�������ʽ�ã� ![]()
������������Ϊ![]() ��ͼ��
��ͼ��
��2����ͼ��֪�� ![]() ʱ��
ʱ�� ![]() ����3����
����3����![]() �����������
�����������
��3����![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ��
��![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��
��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����1��4��������3��0���ֱ�������ʽ�ã�
![]()
���![]()
��������ʽΪ![]()
��![]() ʱ��
ʱ�� ![]()
��P��������0��3����

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�