Question

【题目】如图，在平行四边形ABCD中，E，F为对角线BD上的两点，且∠DAE＝∠BCF．

求证：（1）AE＝CF；

（2）四边形AECF是平行四边形．

Answer 1

【答案】（1）详见解析；（2）详见解析

【解析】

（1）根据平行四边形的性质可得AB＝CD， AB∥CD，得证∠BAE＝∠DCF，可以证明△ABE≌△DCF（ASA），从而得出AE＝CF；

（2）根据全等三角形的性质可得∠AEB＝∠CFD，根据等角的补角相等可得∠AEF＝∠CFE，然后证明AE∥CF，从而可得四边形AECF是平行四边形．

（1）∵四边形ABCD是平行四边形，

∴AB＝CD，∠DAB＝∠BCD，AB∥CD，

∠ABE＝∠CDF．

∵∠DAE＝∠BCF，

∴∠BAE＝∠DCF．

在△ABE和△CDF中，

，

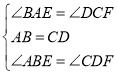∴△ABE≌△DCF（ASA）．

∴AE＝CF．

（2）∵△ABE≌△DCF，

∴∠AEB＝∠CFD，

∴∠AEF＝∠CFE，

∴AE∥CF，

∵AE＝CF，

∴四边形AECF是平行四边形．