题目内容
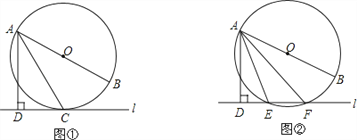
【题目】如图,△ABC内接于⊙O,过点A作⊙O的切线,交OC的延长线于点D,∠D=30°
(1)求∠B的度数;
(2)若OD⊥AB,BC=5,求AD的长.

【答案】(1)30°;(2)![]()
【解析】试题分析:(1)连接OA,由AD为![]() 的切线,利用切线的性质得到OA与AD垂直,得到
的切线,利用切线的性质得到OA与AD垂直,得到![]() 为直角三角形,利用直角三角形的两锐角互余求出
为直角三角形,利用直角三角形的两锐角互余求出![]() 的度数,再利用同弧所对的圆心角等于所对圆周角的2倍,即可求出
的度数,再利用同弧所对的圆心角等于所对圆周角的2倍,即可求出![]() 的度数;
的度数;
(2)由OD⊥AB,,利用垂径定理得到![]() ,利用等弧对等弦得到AC=BC=5,由
,利用等弧对等弦得到AC=BC=5,由![]() ,利用30°所对的直角边等于斜边的一半得到OA为OD的一半,而OC=OA,可得出C为OD的中点,求出OD的长,再利用勾股定理即可求出AD的长.
,利用30°所对的直角边等于斜边的一半得到OA为OD的一半,而OC=OA,可得出C为OD的中点,求出OD的长,再利用勾股定理即可求出AD的长.
试题解析:(1)连接OA,
∵AD为![]() 的切线,
的切线,
![]() 又
又![]()
![]()
∵∠AOD与∠B所对的弧都为![]() .
.
∴∠AOD=2∠B,
则![]()
(2)∵OD⊥AB,
∴![]() ,
,
∴AC=BC=5,
![]()
![]() 即C为OD的中点,
即C为OD的中点,
![]()
即OD=2AC=10,
则根据勾股定理得: ![]()


练习册系列答案
相关题目
【题目】苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
贝类产品 | 0.9 | 0.3 | 0.33 |
蟹产品 | 0.4 | 1 | 2 |
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?