题目内容
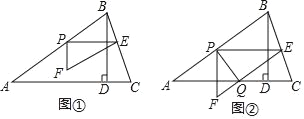
【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
【答案】(1)5;(2)当0<t≤1时,S=![]() t2+
t2+![]() t;当
t;当![]() ≤t<5时,S=
≤t<5时,S=![]() (5﹣t)2;(3)①
(5﹣t)2;(3)①![]() 或
或![]() ;②
;②![]() 或
或![]() .
.
.
【解析】试题分析:
(1)在Rt△ABD中,由∠BDA=90°,AB=5,BD=3,可由勾股定理求得AD=4;在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,可求得CD=1;由此可得AC=AD+CD=5;
(2)由题意分析可知,如图1,当点D在线段EF上或EF的下方时,△PEF与△ABD重叠部分图形为矩形PMDN;如图2,当点F落到AC上或AC的上方时,△PEF与△ABD重叠部分图形为四边形PMFN;分这两种情况分析讨论即可;
(3)①如图3、图4,分I、S△PFQ:S△PEQ=1:2和II、 S△PFQ:S△PEQ=2:1两种情况讨论,由此可分别可得到:S△PEQ:S△PEF=2:3和S△PEQ:S△PEF=1:3从而可得:PG:PF=2:3和PG:PF=1:3,结合PG= ![]() ,PF=
,PF=![]() 即可解得所求AP的长;
即可解得所求AP的长;
②如图5、图6,分I、PQ的垂直平分线经过当点A和II、PQ的垂直平分线经过点B两种情况分析讨论即可求得对应的t的值.
试题解析:
(1)在Rt△ABD中,∠BDA=90°,AB=5,BD=3,
∴AD=![]() ,
,
在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,
∴CD=![]() ,
,
∴AC=AD+CD=4+1=5.
(2)如图1中,当0<t≤1时,重叠部分是四边形PMDN.
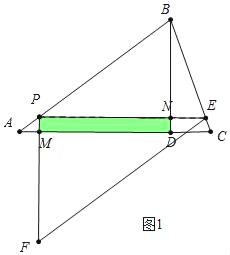
易知PA=t,AM=![]() t,PM=
t,PM=![]() t,DM=4﹣
t,DM=4﹣![]() t,
t,
∴S=![]() t(4﹣
t(4﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t.
t.
如图2中,当![]() ≤t<5时,重叠部分是四边形PNMF.
≤t<5时,重叠部分是四边形PNMF.

∵AB=5,AC=AD+CD=4+1=5,
∴AC=AB,
易证PB=PE=5﹣t,PF=![]() (5﹣t),PN=
(5﹣t),PN=![]() (5﹣t),
(5﹣t),
S=![]() (5﹣t)
(5﹣t)![]() (5﹣t)﹣
(5﹣t)﹣![]() (5﹣t)
(5﹣t)![]() (5﹣t)=
(5﹣t)=![]() (5﹣t)2.
(5﹣t)2.
(3)①如图3中,PF交AC于G.
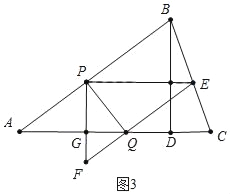
当S△PFQ:S△PEQ=1:2时,
∴S△PEQ:S△PEF=2:3,
∴![]() PEPG:
PEPG: ![]() PEPF=2:3,
PEPF=2:3,
∴PG:PF=2:3,
∴![]() t:
t: ![]() (5﹣t)=2:3.
(5﹣t)=2:3.
∴t=![]() ,即AP=
,即AP=![]() .
.
如图4中,当S△PFQ:S△PEQ=2:1时,
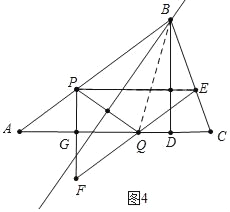
∴S△PEQ:S△PEF=1:3,
∴![]() PEPG:
PEPG: ![]() PEPF=1:3,
PEPF=1:3,
∴PG:PF=1:3,
∴![]() t:
t: ![]() (5﹣t)=1:3.
(5﹣t)=1:3.
∴t=![]() ,即AP=
,即AP=![]() ,
,
∴AP的值为![]() 或
或![]() .
.
②如图5中,当PQ的垂直平分线经过当A时.
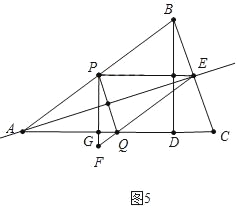
易知四边形APEQ时菱形,
∴PE=PA,即t=5﹣t,
∴t=![]() .
.
如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.
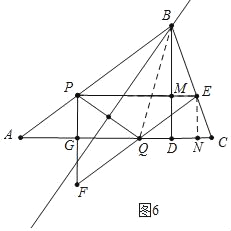
易知四边形PENG时矩形,四边形DMEN时矩形,
∴PG=EN=![]() t,EM=DN=PE﹣PM=
t,EM=DN=PE﹣PM=![]() (5﹣t),
(5﹣t),
QN=![]() EN=
EN=![]() t,
t,
∴QD=![]() t﹣
t﹣![]() (5﹣t)=t﹣1,
(5﹣t)=t﹣1,
在Rt△BQD中,∵BQ2=QD2+BD2,
∴(5﹣t)2=32+(t﹣1)2,
∴t=![]() .
.
综上所述,t=![]() s或
s或![]() s时,PQ的垂直平分线过△ABC的顶点.
s时,PQ的垂直平分线过△ABC的顶点.

 名校课堂系列答案
名校课堂系列答案