题目内容
【题目】请把下列的证明过程补充完整:

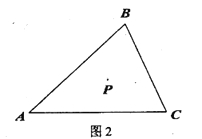
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠______
∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠______
∴∠3=∠______(等量代换)
∴AD∥BE______.
【答案】BAF,BAF,DAC,DAC,内错角相等,两直线平行.
【解析】
根据平行线的性质求出∠4=∠BAF=∠3,求出∠DAC=∠BAF,推出∠3=∠DAC,根据平行线的判定推出即可.
证明:∵AB∥CD,
∴∠4=∠BAF(两直线平行,同位角相等),
∵∠3=∠4,
∴∠3=∠BAF,
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC,
∴∠3=∠DAC,
∴AD∥BE(内错角相等,两直线平行),
故答案为:BAF,BAF,DAC,DAC,内错角相等,两直线平行.

练习册系列答案
相关题目